고정 헤더 영역
상세 컨텐츠
본문
1. 미분의 이해
수학 단원에서 미분의 개념을 이해하는 방법으로 저는 "지구 전체와 지금 현재 여러분 가장 가까이 있는 사람과의 관계"라고 설명을 합니다. 지구는 둥글다는 전제에 동의한다면 지구의 모습은 거대한 원에 해당합니다. 곡선의 형태를 지니고 있다는 말이 됩니다.
그런데 여러분 가장 가까이 있는 사람과의 거리를 생각해 보면 직선이 됩니다. 거대한 지구라는 원에 비하면 여러분의 가장 가까이 있는 사람과의 거리가 만약 1m 정도라고 하더라도 직선에 해당합니다. 이 개념을 '극한(limit)'이라고 보통의 수학 교과에서는 설명하고 있습니다. 지구라는 거대한 원에서 좁히고 좁혀서 여러분과 여러분 옆에 있는 사람까지 가는 상태를 '극한'으로 가는 상태가 됩니다.
이것을 수학으로 표현하면 두 사람 사이의 거리는 직선으로 표현되면서 동시에 기울기를 갖게됩니다. 지구라는 거대한 원을 이루는 아주 작은 부분에 해당하기에 기울기의 정도가 거의 없다고 하더라도 기울기는 존재하는 것입니다. 이 상태가 되면 직선이므로 두 지점 간의 기울기를 구할 수 있게 되는 것입니다.
원래는 거대한 원이었지만, 극한의 상태가 되면서 '직선'이 되고, 두 지점 사이의 직선은 기울기를 갖습니다.
2. 평균변화율, 도함수
현재 수학에서 미분과 관련되어 이해하는 방법으로 다음과 같은 기호를 사용하여 나타내고 있습니다.
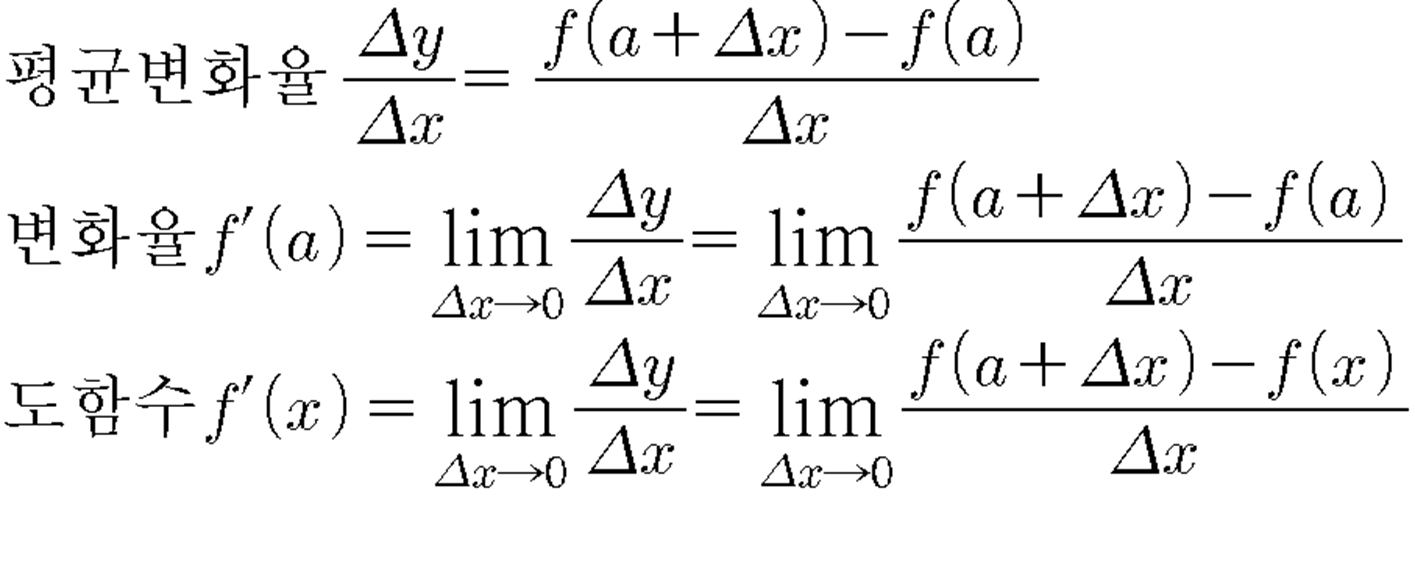
수학의 기호에서 사용되는 위의 복잡해보이는 기호들은 일종의 언어 논리를 갖추고 있습니다. 기호화의 과정에서 미분이 지닌 본래적 의미가 드러나고 있음을 볼 수 있습니다.
평균변화율 : 위의 도표에서 보여지는 평균변화율은 삼각형 모양의 기호(delta)를 사용하고 있습니다. Delta는 '증가량'이라는 말의 기호화입니다. 따라서 'x의 증가량'에 해당하는 것을 기호화하면 'delta x'가 됩니다. 마찬가지로 y의 증가량에 해당하는 것을 기호화하면 'delta y'로 표현할 수 있고, 이때 삼각형 모양의 기호가 '증가량'이라는 언어 표현을 대신하고 있음을 볼 수 있습니다.
'극한'에 해당하는 의미로 limit에서 줄임말인 lim을 사용합니다. 위의 기호 표시에서 lim이 그 역할을 하는 것입니다. 그리고 증가량이 거의 0에 가깝다는 의미로 위에서는 'x의 증가량이 거의 o'에 가깝다고 표현하는 것을 볼 수 있습니다. 이 지점이 앞에서 말한 거대한 지구에서 한 점도 찍기 어려운 옆 사람과의 거리에 해당합니다.
또한 f라는 기호는 funtion의 첫 글자입니다. 우리말에서는 '함수'라고 표현하는 것입니다. 위의 도표에서 보면 f(x)나 f(a)는 함숫값을 의미합니다. 즉 어떤 함수식에 a나 x를 대입했을 때 나오는 값이라는 의미를 갖는 것입니다. 또한 함수에서 사용되는 delta x에 해당하는 값은 원래의 값에서 증가한 x값이라는 의미를 갖게 됩니다.
3. 수학 기호가 가진 세계적 보편성
우리 인류가 가진 기호 체계 중에서 수학이라는 학문으로 한정해서 본다면 각각의 기호는 전 세계인이 공통으로 사용하는 방식으로 기능을 하고 있습니다. 어느 나라를 막론하고 공통의 단원을 기호화하여 이해한다고 하면 수학에서 사용하는 기호 역시 같은 의미를 전달할 수 있습니다.
우리가 일상생활에서 사용하는 알파벳이라는 문자기호가 전 세계인이 공통으로 이해할 수 있는 것처럼, 수학 기호 역시 적당한 교육이 이루어졌다면, 관련 기호가 갖는 의미를 파악할 수 있을 것입니다.
수학의 미분 단원에서 다루는 기호는 비록 국가마다 사용하는 언어가 다르기 때문에 설명하는 언어 표현은 다를지라도, 그 안에 담긴 의미를 기호화하여 이해할 수 있을 것입니다.
'기호 언어학' 카테고리의 다른 글
| 좌표와 코디 coordinate : meaning, synonyms (0) | 2023.07.23 |
|---|---|
| 기호 언어학으로 보는 상표와 지식 재산 (0) | 2023.07.22 |
| 영어 줄임 말과 줄임 글자의 기호학, (0) | 2023.07.21 |
| 로마 숫자, 아라비아 숫자 기호의 유래와 의미 (0) | 2023.07.21 |
| Root(루트)기호에 담긴 언어적 의미와 계산 원리 (0) | 2023.07.20 |





